How does Recursion work? Recursion vs Iteration
Recursion and iteration are the fundamental methods for repeating and processing a given set of commands in every programming language. So every programmer must be conversant with these concepts. Many software engineering interview concerns may be solved using basic recursion.

Suppose you have to sort 200 documents with names in the correct alphabetical order. What you’ll most certainly do is first arrange all the documents into different piles based on the first letter of the names. Then you’ll take each pile and arrange the documents alphabetically, exactly how the words are arranged in the dictionary. After you’ve done that, you can then merge all the piles on top of one another, starting possibly with the letter A to Z.
You could also have taken a different approach but this process was more convenient.
What you did here was you broke down a large problem into smaller subproblems and solved each of them separately to reach the bigger solution. This is recursion.
Still not clear? Wait, we can’t leave you like that.
A child couldn't sleep, so his mother told him a story about a little pup,
who couldn't sleep, so the pup's mother told him a story about a little bear,
who couldn't sleep, so the bear's mother told him a story about a little panda,
who fell asleep. And the little bear fell asleep; the little pup fell asleep; the child fell asleep.
We hope now you have understood things better. If still not, nothing to worry about. We’ll be making it easier for you and take your mind on a journey to understand recursion throughout this blog using different examples and use cases.
If you happen to search for ‘recursion’ on google, you’ll see the ‘Did you mean recursion?’ message. Click on that and it’ll open the same page again and again.
Maybe it’s google’s way of defining recursion for you.
In a nutshell, recursion is the repeated application of a recursive process. Whatever that means, right? If we delve into more detail- recursion is a process of solving a computational problem where the solution relies on solutions of smaller versions of the same problem. It uses functions that call themselves from within their own code. Read on to learn more about Recursion and Iteration, as well as how they differ from one another.

What is recursion?
Recursion is referred to as the process through which a function regularly calls itself. Selection structure is used in recursion. An endless recursion happens if the recursion step does not reduce the issue in a way that converges on some condition, known as the base condition. An endless recursion can cause the system to crash. When a base case is detected, the recursion ends.
When Should You Use Recursion?
We occasionally come upon a situation that is too difficult to tackle immediately. In most situations, we strive to divide such difficulties into smaller chunks. Then we can figure out how to tackle these smaller bits and then piece together a solution to the larger challenge. This is the complete concept of recursion.
Recursion occurs when a function calls itself, directly or indirectly, and the function that calls itself is called a recursive function. It is mostly employed when a larger problem's solution can be described in terms of smaller issues.
A real-world example of Recursion
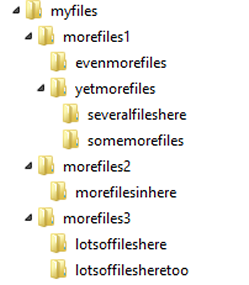
Assume, you need to locate a file on your computer. You don't want to look for it manually, and you figure it's a good workout in and of itself, so you'll develop a function to do it for you. How do you go about it?
Let's begin with the root directory. Then we need to choose one of the kids and look inside. That child may have children of its own, so we must delve deeper and deeper until there are no more children. Then we return and try one of the other kids.
What exactly did we just do?
Our code might look something like this:
func search(currentDir):
if targetFile in currentDir:
return currentDir
for childDir in currentDir:
result = search(childDir)
if result != null:
return result
return nullWe began in our current directory and then called each child directory recursively. Our function within itself was named to look through the child directory.
Essentially, we are conducting a depth-first search.
This is a fairly simplistic example, but it demonstrates a crucial point: recursive structures exist all around us.
When we have a hierarchical structure, the simplest way for us to parse through that structure is to use recursion.
It allows us to quickly maintain track of what we've already traversed and saves us the trouble of having to keep track of which directories we've previously visited. We can follow a well-defined progression across our directories.
This is possible because the recursive function stores all the steps in a memory stack.
In a recursive program, we need a base case whose solution is provided. Think of the sleeping panda in the above example. If it wasn’t sleeping the loop wouldn’t stop.
What is a base case condition in recursion?
Base Case- This is essentially your desired end result. When this condition is met, return your final result, and the function is completed.
We can understand the base case better by taking the example of a factorial function.
int fact(int n)
{
if (n < = 1) // base case
return 1;
else
return n*fact(n-1);
}
Here, the base case for n<= 1 is defined, and a larger factorial can be converted into smaller subproblems until we reach the base case. So, the base case terminates the recursive function.
But why recursion?
Why do we need recursion?
As we’ve seen, recursion is a useful tool for solving problems that can be expressed in terms of smaller versions of themselves.
- In general, recursion is best used for problems with a recursive structure, where a problem can be broken down into smaller versions. Iteration, on the other hand, is better suited for problems that can be solved by performing the same operation multiple times on a single input.
- Recursion also provides code redundancy, making code reading and maintenance much more efficient. Understanding recursion thoroughly can lead to genuine mastery of functional programming languages, allowing programmers to code specific programs quickly. Because some issues are intrinsically recursive, knowing recursive functions might help you solve them faster.
- Furthermore, recursion is useful and required in many applications involving complex algorithms, such as tree and graph traversal. The key to a wonderful coding experience is understanding the applications of recursion in data structures and how to properly use recursion to manipulate functions in diverse systems.
Recursion can be a more elegant and efficient solution for certain types of problems, such as those that involve searching or traversing a complex data structure. However, it can also be more difficult to understand and debug than iteration and can be less efficient in terms of time and space complexity if not implemented carefully.
Therefore, the decision of whether to use recursion or iteration for a particular problem depends on the specific problem and the desired characteristics of the solution. In general, it is often a good idea to try solving a problem using both approaches and compare the results to determine which is more effective in a given situation.
To understand everything about recursion in-depth, you can refer to this 3-hour tutorial by Masai's senior curriculum engineer, Venugopal Panchumarthi-
What is iteration?
Iteration is referred to as the process of repeating a computational or mathematical method till its regulating circumstance becomes untrue. It employs a repetition structure. If the loop condition test never becomes untrue, iteration results in an eternal loop. This indefinite looping consumes CPU cycles on a regular basis. When the loop condition fails, the iteration ends. Iteration uses less memory but lengthens the code, making it tougher to comprehend and write.
When Should You Use Iteration?
Iteration is a manner of continually executing a sequence of instructions until the condition controlling the loop turns false. It consists of initialisation, comparison, statement execution within the iteration, and updating the control variable. It is critical to have the correct controlling condition during iteration; otherwise, the program may fall into an infinite loop.
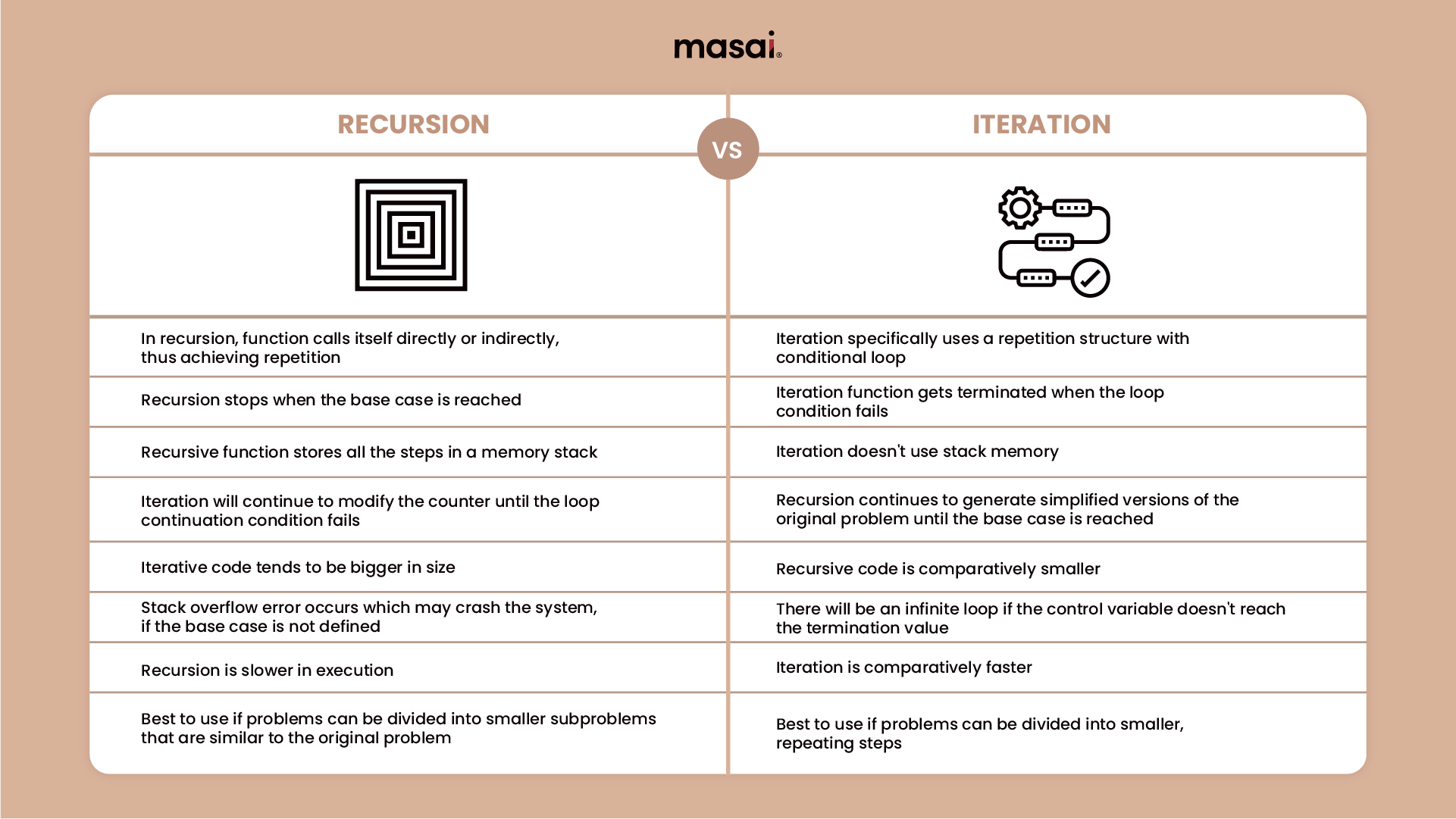
Recursion vs Iteration
“But doesn’t iteration seem almost similar?”
No, it’s not. Iteration uses conditional loops such as a ‘for loop’ to run a set of instructions repeatedly until the condition of the iteration statement becomes false.
While recursion, as we know keeps calling a function itself within its own code until it meets the base case.
Imagine there is a line of n students, each holding a piece of paper with a number written on it. There is another student, who wants to know the sum of each
There are two ways to solve this problem,
- Either the student goes to each of the n students and sums up the number. This is called iteration.
- Another approach can be as follows- Let the first student pass his paper to the one sitting behind him. Now this student, who just got the paper from the first student, adds both numbers and passes it to the student behind him. This is recursion.
Here are a few more differences between recursion and iteration-
When should you recurse and when should you loop?
Recursion is really useful for operating on things that have many possible branches and possibilities, and are too complicated for adopting an iterative method.
Remember the root folder and target file example we mentioned earlier? Recursion works well for this type of structure because it allows you to search various branching pathways without having to include numerous checks and conditions for each possibility.
Trees and graphs are the kinds of structures where using recursion makes the most sense.
That being said, recursion can increase memory usage. Let’s go back to the factorial example we took earlier. Every time we add a new recursive call to the stack, there’s an increase in the time and space complexity.
Now, for many small projects, this might be an okay price to pay but once the program starts making too many recursive calls then you might want to think about the impact of the large call stack.
Also, recursion can be more difficult to understand and debug than iteration. This is because, in a recursive function, the same code is executed multiple times with different input values, which can make it hard to keep track of what's happening. On the other hand, iteration uses a loop to repeat a set of instructions, which can be easier to understand and debug.
In general, it's best to use recursion when the problem you're trying to solve can be divided into smaller subproblems that are similar to the original problem, and iteration is best for problems that can be divided into smaller, repeating steps. It's also worth noting that some problems can be solved using either recursion or iteration, and in those cases, it often comes down to personal preference.
Advantages of Recursion
- Recursion makes the code simpler to comprehend and follow, which improves code readability.
- By dividing difficult issues into smaller, easier-to-manage subproblems, recursion can make complex problems simpler.
- Recursion gives programmers a versatile and effective tool to utilise, which can aid in problem-solving.
- Recursion can reduce the amount of code required to solve a problem, which can save time and space.
- Recursion makes it possible to store and retrieve data more effectively, which facilitates efficient data processing.
Types of Recursion
Direct Recursion
In direct recursion, functions call themselves. This process comprises a single-step recursive call by the function from within its own body.
Let’s understand this through the code to compute the square of a given number-
#include <iostream>
using namespace std;
// recursive function to calculate the square of a number
int square(int x)
{
// base case
if (x == 0)
{
return x;
}
// recursive case
else
{
return square(x-1) + (2*x) - 1;
}
}
int main() {
// implementation of square function
int input=30;
cout << input<<"^2 = "<<square(input);
return 0;
}
Indirect Recursion
Indirect recursion is where a function calls another function to call the original function. Meaning, function f1 calls a new function f2 and f2 calls the initial function f1 in return. This is a two-step recursive process as the function calls another function to make a recursive call.
Let’s see how to print all the numbers between 15 to 27 using indirect or mutual recursion-
using namespace std;
int n=15;
// declaring functions
void foo1(void);
void foo2(void);
// defining recursive functions
void foo1()
{
if (n <= 27)
{
cout<<n<<" "; // prints n
n++; // increments n by 1
foo2(); // calls foo2()
}
else
return;
}
void foo2()
{
if (n <= 27)
{
cout<<n<<" "; // prints n
n++; // increments n by 1
foo1(); // calls foo1()
}
else
return;
}
The output would display this:
15 16 17 18 19 20 21 22 23 24 25 26 27
Tail Recursion
A function is said to be tail-recursive if no operations are pending when the recursive function returns to its caller.
Such functions, immediately return the return value from the calling function.
It is an efficient method as compared to others, as the stack space required is less and even compute overhead will get reduced.
Here’s the implementation of tail recursion in JavaScript-
// Javascript code Showing Tail Recursion
// Recursion function
function fun(n)
{
if (n > 0)
{
document.write(n + " ");
// Last statement in the function
fun(n - 1);
}
}
// Driver Code
var x = 3;
fun(x);
Output: 3 2 1
Non-tail Recursion
Non-tail Recursion is a recursive function in which the first statement is a recursive call followed by the other operations.
It is also known as Head Recursion.
Non-tail Recursion does not perform any operations throughout the recursive calling process. Instead, all operations are completed at the time of return.
Here’s an example-
// JavaScript program showing Head Recursion
// Recursive function
function fun(n)
{
if (n > 0) {
// First statement in the function
fun(n - 1);
document.write(" "+ n);
}
}
// Driver code
var x = 3;
fun(x);
Output: 1 2 3
Wrapping Up
So, this should wrap this piece on recursion. No doubt, it's a tricky concept but we hope we were able to provide you a decent understanding. On that note, here are a few key points that we've have learned throughout the article:
- Recursion involves a function calling itself in order to solve a problem or accomplish a task
- Recursive functions have a recursive case condition that calls the function again, and a base case condition that stops the recursion from continuing indefinitely
- Recursive functions stores all the steps in a memory stack. In case, a base case is not defined, it can also cause a stack overflow error
- It is useful for operating on things that have many possible branches and possibilities, on complex data structures like trees and graphs
- Iteration uses conditional loops to run a set of instructions repeatedly until the condition statement becomes false
- Iteration is comparatively faster in execution, and the best fit for solving problems that can be divided into simpler repetitive steps
More resources on data structures and algorithms-
- Data structures and Algorithms- Explained with Examples
- Array Data Structure- Explained with Examples
- Queue Data Structure- Applications, Types, JavaScript Implementation
- 12 Must-Know Algorithms For Programmers
- A Step-By-Step Guide to Becoming a DSA Expert
Happy learning!
FAQs
Why is a recursion method preferable to iteration?
Recursion is considerably superior to iteration for problems that can be divided into numerous smaller sections. The divide and conquer strategy, when combined with recursion, can reduce the size of your issue at every stage and take a shorter time than a simple iterative approach.
Is it possible to transform every recursion into an iteration?
By substituting recursive calls with iterative control structures and resembling the call stack with a stack explicitly maintained by the program, any recursive function may be turned into an iterative function.

