Applications of Tree Explained
In this article, we have explained the applications of trees in detail instead of covering them just in bullet points.
A tree is a hierarchical data structure composed of nodes connected by edges, each of which has a value and a list of pointers to other nodes. (This is similar to how parents refer to their offspring in a family tree).
Unlike stacks and queues that store data in a linear fashion, trees are used to represent hierarchical data. It begins with a root point and then expands across numerous elements in a hierarchical structure.
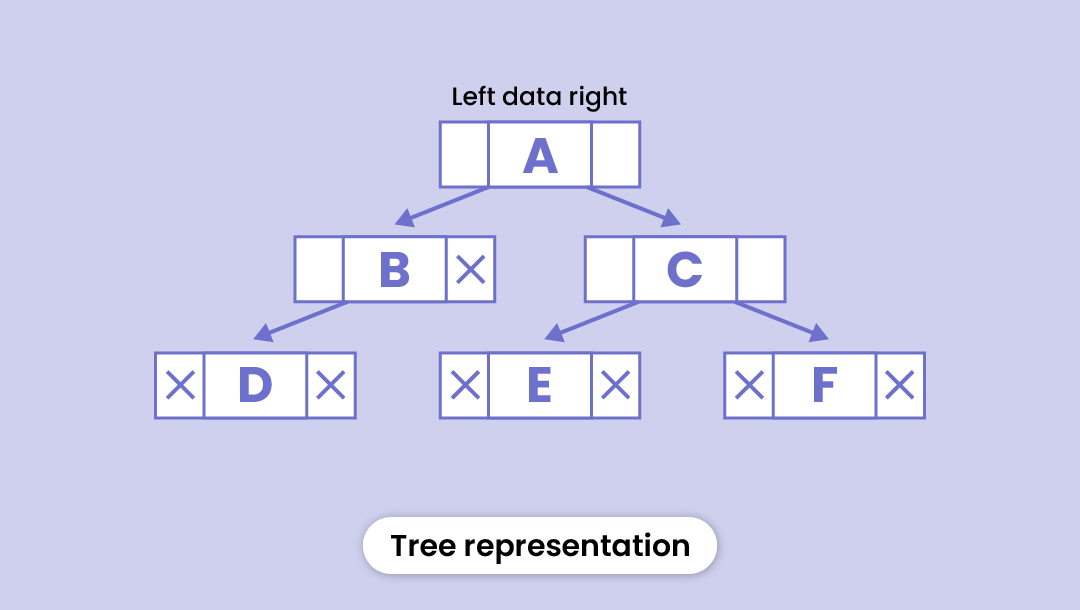
If you still can't picture it, imagine an upside-down tree (literally, a tree). It grows from the root and then sprouts many branches at various heights. That is how a tree data structure appears.
But why do we need different data structures? What’s the point of having multiple data structures like stacks, queues, arrays, linked lists, and then trees?
Choosing a data structure depends on the following factors:
- What type of data must be stored?: It is possible that a specific data structure will be the greatest fit for some type of data.
- Cost of operations: Of course, we’d want to reduce the cost of the most common procedures. For instance, if we have a simple list on which to execute the search, we can create an array in which the elements are stored in sorted order to perform the binary search. Because it cuts the search space in half, the binary search is highly quick for basic lists.
- Time and space complexity- Which data structure will take lesser time and space to perform the required operations? For example, accessing an element is much easier in the case of an array that has a time complexity of 0(1) compared to a linked list that has a time complexity of 0(n). But when it comes to inserting an element, the linked list is the preferable option. (Know more about array vs linked list[1])
So, these are the reasons why we need different data structures for different situations.
Why trees?
Tree data structures are useful because they allow you to store and organize data in a hierarchical and logical manner. Here are some of the reasons we need tree data structures:
Effective data searching and sorting: Tree data structures enable efficient data searching and sorting. We can swiftly identify and obtain the data we need by employing various methods such as binary search or depth-first search.
Simple insertion and deletion: Tree data structures make it simple to add and remove nodes. Tree architectures, unlike other data structures like arrays and linked lists, may easily absorb changes without requiring large alterations.
Organization and hierarchy: Tree structures are very useful for organizing data that has a natural hierarchy, such as file systems or company hierarchies.
Recursive algorithms: Many algorithms that work on trees are recursive in nature, making them simple to develop and understand.
We have already covered the different types of trees, operations, implementation, and more in our previous article. Here, we will discuss their real-world applications.
Applications of tree data structure
- Storing naturally hierarchical data
- Databse indexing
- Parsing
- Artificial Intelligence
- Cryptography
Let's cover each of them in detail:
Storing naturally hierarchical data
This includes a large amount of real-world data. Consider your computer's file system, for example. The files and folders are organized hierarchically, with a root folder (typically designated by /) at the top.
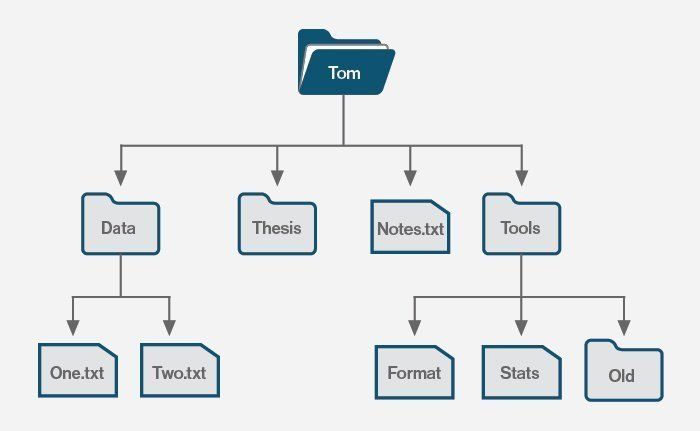
Each subdirectory can have other subfolders, and so on. When storing such data, a tree data structure is the most intuitive approach to do so.
Database indexing
Heard of Database applications? They are software programs designed to interact with databases. They allow users to store, retrieve, update, and manipulate data within a database and can be used for purposes like managing inventory, storing customer information, or tracking financial transactions.
Database applications include the following qualities in their most general form:
- Large collections of frequently updated records.
- A single key or a combination of keys is used to search.
- Use of key range queries for min/max searches.
One option to store primary and secondary key indices is to use the binary search tree (BST).
BSTs can store duplicate key values, and run efficient insertion, deletion, search, and efficient range queries. When sufficient main memory is available, the BST can be used to implement both primary and secondary key indices.
Database indexing allows us to reduce the number of rows/records that must be inspected when we run a select query with a 'where' clause.
B-trees are the most often used index data structures because they are fast for lookups, deletions, and insertions. All of these operations are possible in logarithmic time.
R-tree[2] is frequently used in spatial databases. It helps with searches like "list all the coffee shops within 2 miles of my location".
Parsing
Parsing is the process of breaking down code into its constituent pieces using grammar. The resulting data structure is often a tree-like structure known as an abstract syntax tree (AST), which describes the syntax of the code.
It's a fundamental process in computer science and is used in many different areas, such as compilers, interpreters, text editors, and data processing.
The parsing process consists of numerous steps, including:
Lexical analysis: The initial stage in parsing is to divide the input text into tokens, which are the basic units of meaning in the computer language, and feed the tokens into the parser.
Syntax analysis: The parser then analyses the input tokens with a grammar to construct an abstract syntax tree (AST) that describes the syntax of the code. The grammar defines the programming language's structure and rules, as well as how tokens should be joined to generate valid expressions, statements, and other language constructs.
Semantic analysis: Now the parser can do semantic analysis to ensure that the code is accurate. This includes looking for type errors, undefined variables, and other logical problems that aren't identified during syntax analysis.
Code generation: If the code is accurate and passes the semantic examination, the parser can generate machine code or bytecode that a computer can execute.
As you can see, trees are a fundamental tool for parsing and are widely used in a variety of applications, from compilers to natural language processing.
Artificial Intelligence
Trees are widely used in artificial intelligence, particularly in the field of machine learning. They are used in various algorithms to model complex relationships between inputs and outputs and to classify and make predictions.
Some examples of tree-based algorithms include-
Decision Trees: A decision tree is a graphical representation of all possible solutions to a decision. They are widely used for classification and regression tasks in machine learning.
Random Forests: A random forest is an ensemble of decision trees that are trained on different subsets of the data and then combined to make a final prediction. They are considered to be one of the most accurate machine-learning algorithms.
Gradient Boosting Trees: Gradient boosting trees are an ensemble of decision trees that are trained using a boosting algorithm. Boosting algorithms work by training the model on the errors from the previous iteration, leading to a model that is highly accurate for complex data sets.
XGBoost: XGBoost (Extreme Gradient Boosting) is an optimized version of gradient boosting trees that are widely used for Kaggle competitions[3] and other data science tasks.
In addition to these algorithms, trees are also used in other areas of artificial intelligence, such as in-game trees for decision-making in games and decision support systems[4], and in hierarchical reinforcement learning algorithms for training agents in complex environments.
Cryptography
Trees are widely used in cryptography to provide integrity and authenticity guarantees for data transmitted over a network. Cryptographic trees, such as Merkle trees[5], allow a receiver of data to verify that the data has not been tampered with during transmission.
Here's a detailed explanation of how trees are used in cryptography:
Hash Functions: Cryptographic trees rely on hash functions to provide integrity guarantees for data. A hash function takes an input and produces a fixed-length output, known as a hash value or digest. It is designed to be a one-way function, meaning that it is computationally impossible to recreate the input from the hash value.
Merkle Trees: A Merkle tree is a binary tree structure in which each leaf node is a hash value of a block of data, and each non-leaf node is a hash value of its children. The root of the Merkle tree represents the hash value of all the data in the tree. By including the root hash value in a message, a sender can provide an authenticity guarantee for the data in the tree.
Authentication: To verify the authenticity of the data in a Merkle tree, the receiver of the data needs only to compute the hash values of the blocks of data, and compare them to the hash values included in the message. If the hash values match, the receiver can be confident that the data has not been tampered with during transmission. If the hash values do not match, the receiver can reject the message.
Optimization: Merkle trees can be optimized for efficient authentication. For example, a sender can include only the hash values for the blocks of data that have changed, reducing the amount of data that needs to be transmitted to provide authenticity guarantees.
Security: The security of Merkle trees relies on the security of the underlying hash function. If a hash function is broken, then the security of the Merkle tree is compromised. Additionally, the security of Merkle trees depends on the number of hash values that need to be verified to authenticate the data. A large number of hash values increases the security of the tree, but also increases the computational cost of authentication.
These are the key concepts of how trees are used in cryptography, but there are many variations and extensions of these ideas that have been developed to meet specific requirements.
Wrapping up
So, these were a few applications of tree data structure. Our motive was to explain the applications in detail instead of just writing bullet points. And we hope you were able to understand each of them.
However if you're new to data structures and algorithms, you can refer to this article where we have explained the concept from scratch using real-world examples.
Refer to 'Tree data structure' to learn everything about trees.
References/Important links
[1]- Array vs Linked list
[2]- R-tree

